编者按：推演了模数转换器（ADC）的直方图测试方法，主要推导ADC的主要静态参数。通过以传统定义法测试和直方图法测试进行ATE测试对比。选取AD7656型号通过以ADVANTEST T2000为平台进行直方图测试，和以ADVANTEST T6575为平台进行传统定义法测试，对比四项参数测试数据，并对两种算法测试优劣进行比对。

*参与项目：陕西省重点产业创新链（群）-工业领域：高精度模拟与混合信号集成电路频谱测试技术研究，受理编号：S2020-YF-ZDCXL-ZDLGY-0297

本文主要通过测试机台模拟步进DAC，并且步进DAC 比待测器件高出4 bit，这样ATE 测试机台能够将一个待测ADC 的一个转换码平均分割16 步进，并且转换16 次。从而待测器件理想情况下每位的转换码都会重复出现16 次。直方图测试就是通过统计每个码点出现的次数，与理想情况下码点出现的次数来计算静态参数值。

1 直方图法参数计算

零点误差( EZ ) 与增益误差（ EG ）

图1 以柱状图表示每个转换码点的次数。假设被测器件是n 位，ATE 测试机台内部的DAC 是n+4 位。

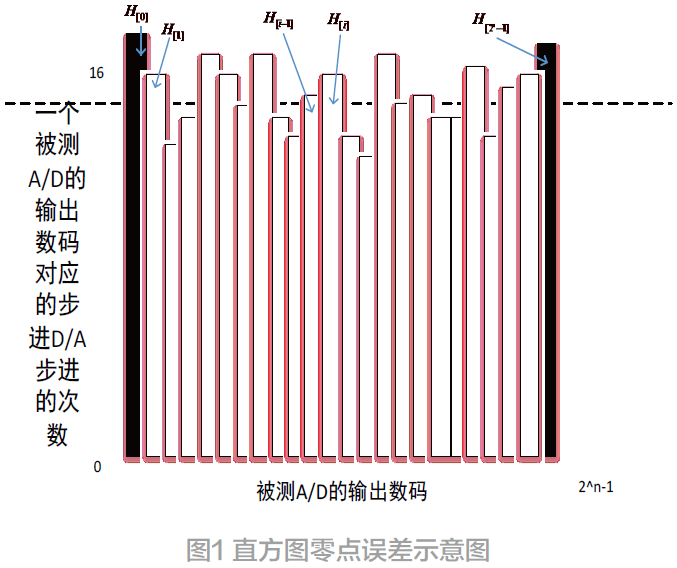
在计算时，先利用ATE 测试机台采集每个转换码i=1到i=2ⁿ−2，重复出现的次数。我们记录转换次数为H。假设每一位转换码在ATE 出现的次数为H(i)。有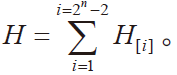

在直方图测试法下有：

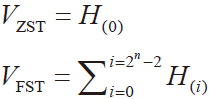
V_ZST是数字输出转换码从00..00 到00..01 时的模拟值。

V_FST是使数字输出转换码从11..10 到11..11 的模拟值。根据待测ADC 静态参数LSBD_OUT 准计算公式

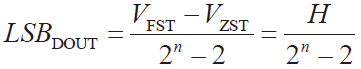
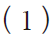
ADC的零点误差：

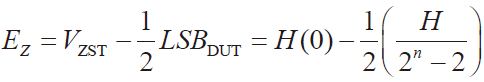
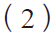
同理增益误差E_G：

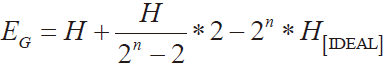
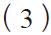
其中， H_[IDEAL] 直方图测试法中理想状态ADC 的输出数码对应的机台步进的次数。

1.2 差分非线性误差 (DNL) 与微分非线性误差 (INL)

根据V_FST、V_ZST的定义，在直方图测试法下有：

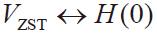
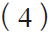
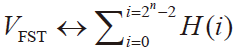
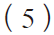
由式(4)(5)相减可以得出

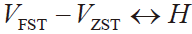
根据A/D 静态参数LSB_DUT准计算公式

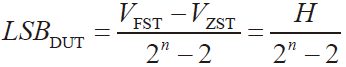
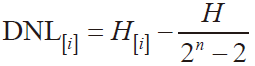
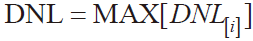
Code Center_[i]为转换码中心是指当数字输出为i时，其1/2 码宽对应的模拟输入值。

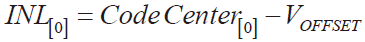
Code Center_[0]是数字转换输出i = 0的，Code Center_[0]就是V_ZS。

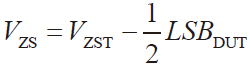
零点的INL值有

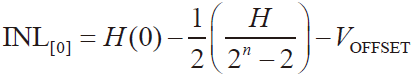
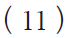
理想的零点INL_[0]=0

当i = 2ⁿ−1(最大值)时，可得

根据ADC静态参数传统计算公式得

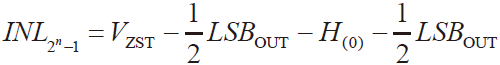
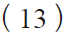
当0 < i < 2n −1时，根据 ADC 静态参数标准计算公式得

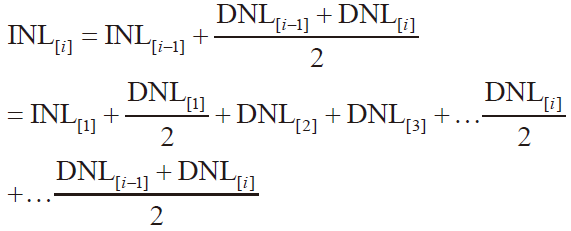
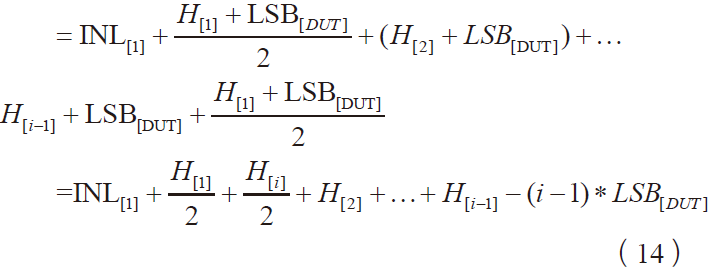
可得

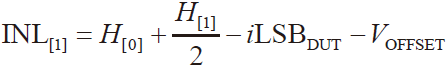
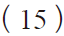
可得直方图测试法INL_[i]的计算公式

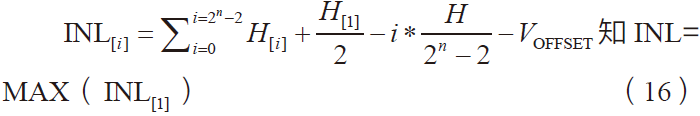
2 测试技术实现

本文选取AD7656BSTZ 型号芯片进行测试分析，分别使用传统定义法测试和基于直方图法测试两种测试方法进行ATE 测试，并分别用这两种测试方法进行算法编写代码，分别计算零点误差、满量程误差、差分非线性误差、积分非线性误差。图2 是器件实物和理想转换示意图。

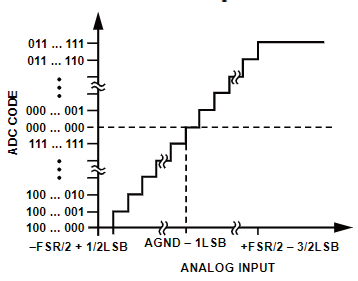
图2 理想转换示意图

2.1 基于传统定义法实现测试

图3是基于ADVANTEST T6575 测试16 位转换码对应的转换值，采样点选取了65 536 个点。该芯片为补码输出，下图为ATE 测试补码输出和转换后测试输出值。ATE将测试的65 536 个转换值抓取到数组中进行传统定义法计算得出E_Z、E_G、DNL、INL 分别为-0.03%FS、0.02%FS、-1.5LSB、1.2LSB。

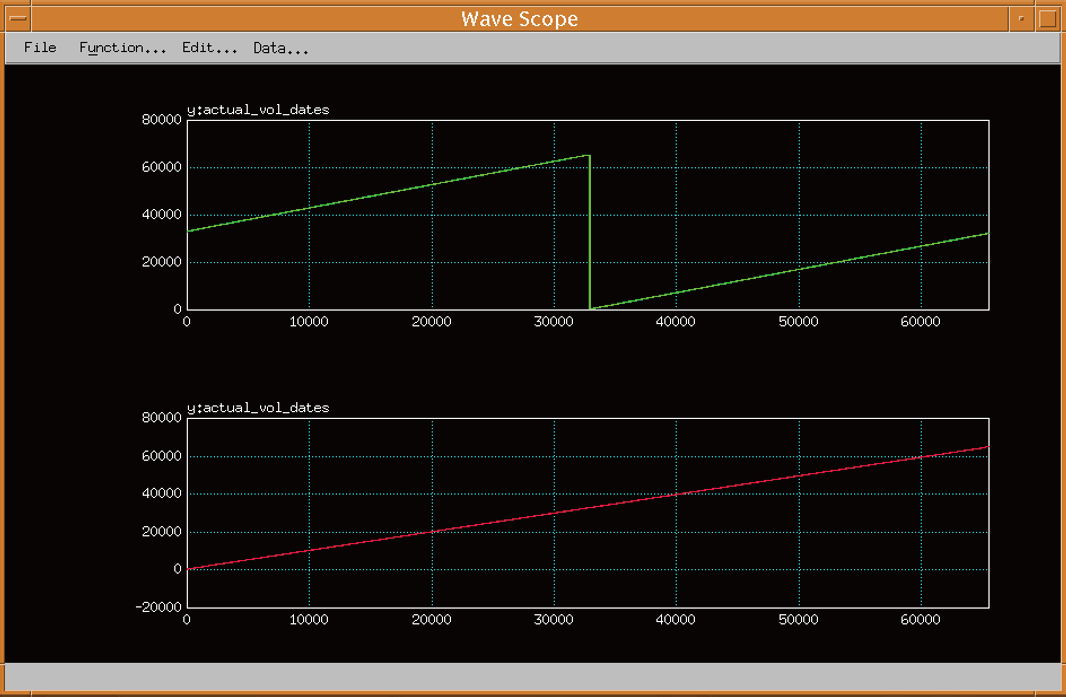
图3 定义测试AD7656BSTZ转换码

2.2 基于直方图法实现测试

图4 图5 是基于ADVANTEST T2000 测试转换输出和DNL测试结果。计算得出E_Z、E_G、DNL、INL 分别为-0.04%FS、0.03%FS、0.6LSB、1.0LSB。

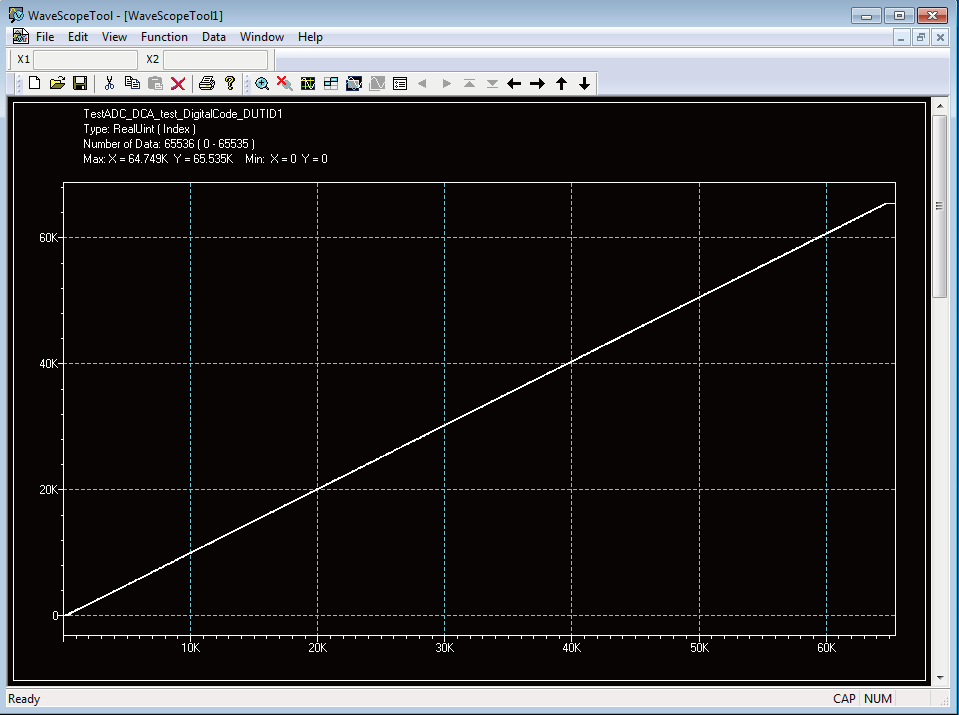
图4 直方图法测试转换码

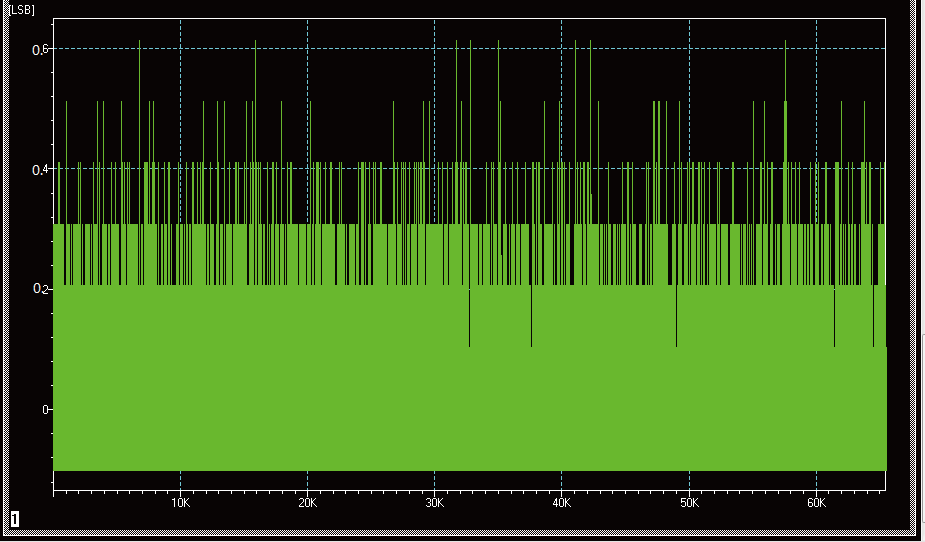
图5 直方图DNL测试结果

3 对比分析

基于传统定义法测试特点首先算法简单容易实现，但是算法计算量较大，其次零点误差和增益误差可直接计算，并且能够直观反映该项参数的指标。直方图法测试特点首先在计算DNL 和INL 可剔除系统干扰或者噪声引起的某个转换点的突变或者丢码。其次直方图法测试需要系统的采样点多，工程上至少1 个转换点需要重复测试16 次，才能保证该算法的优势。但同时也增加了测试时间。

参考文献：

[1] 胡春.基于精度的12位逐次逼近型ADC的研究与设计.华中科技大学硕士学位论文[D].武汉:华中科技大学, 2005,1-2.

[2] 乔高帅.一种高精度逐次逼近模数转换器的研究与设计.上海交通大学硕士学位论文[D].上海:上海交通大学, 2009,13-14.

[3] 孙彤,李冬梅.低功耗逐次逼近数模转换器的研究与设计.清华大学硕士毕业论文[D].北京:清华大学, 2007.

[4] LIU W, CHANG Y, S. K. HSIEN, CHEN B W, LEE Y P, et al. A 600 MS/s 30 mW 0.13um CMOS ADC array achieving over 60 dB SFDR with adaptive digital equalization[J].IEEE ISSCC Dig. Tech. Papers, 2009, 2:82-83.

[5] F KUTTNER. A 1.2-V 10-b 20-Msample/s non binary successive approximation ADC in 0.13-um CMOS[J].IEEE ISSCC Dig. Tech. Papers, 2002,2:176–177.

[6] BASTOS J, STEYAERT M, GRAINDOURZE B, et al. Matching of MOS transistors with different layout styles [J].Icmts 1996-1996 IEEE International Conference on Microelectronic Test Structures, Proceedings, 1996, 17-18.

[ 7 ] A L B I N A C M , H A C K L G . L a y o u t p a r a s i t i c interconnections effects on high frequency circuits[J]. 2007 IEEE Dallas/Cas Workshop on System-on-Chip (Soc): Design, Applications, Integration, and Software, 2007, 71-74.

[8] T WAKIMOTOW, LI H, K. MURASE. Statistical analysis on the effect of capacitance mismatch in a high-resolution successive approximation ADC[J].IEEJ Electrical and Electronic Engineering, 2011, 6(S1). S89-S93.

（本文来源于《电子产品世界》杂志2023年5月期）