编者按：为了提高时栅传感系统的测量精度，本文设计了一种综合运用BP神经网络与灰色模型进行预测的模型。根据激励信号的实际误差引起的测试精度变化，得到预测模型的各项参数。之后建立组合预测模型并设置了健康状况的参考标准。经测试发现，经健康诊断标准判定，健康状况预测结果与电路实际相符。该健康状况预测方法预测精度高，且明显高于单一模型，满足提前准确获悉电路系统健康状况的要求。

时栅传感器是一类根据时空转换位移传感器，其结构简单并且能够满足多种环境的使用要求^[1]。由于在长期使用过程中，电路、信号处理器以及传感器材料都会发生老化，上述情况都会导致测量误差的增加，无法达到高精度测试的状态^[1-2]。为了更深入了解系统运行情况，应对时栅传感器的信号处理系统进行检测，从而提前消除各类潜在故障问题，有效降低损失，确保时栅传感器能够准确测定位移参数^[3-4]。目前的大部分时栅信号处理系统基本都是由模拟集成电路构成，呈现明显的非线性特征，无法获得良好的元件容差性，当电路模块出现故障时，系统激励信号同时存在时变与非平稳信息^[5-8]。

为使模型优势都得到充分发挥，本文设计了一种由灰色模型与BP 神经网络共同构成的能够预测运行健康状况的时栅信号处理系统，确保预测结果可以准确反映系统的健康情况。

1 激励信号误差与测量精度

圆型场式时栅结构见图1 所示。位于转子线圈与传感器定子间会产生匀速旋转磁场，使动测头与定测头导线感应产生电信号，表示各自的空间位置，体现了被测单元的角位移参数^[9]。

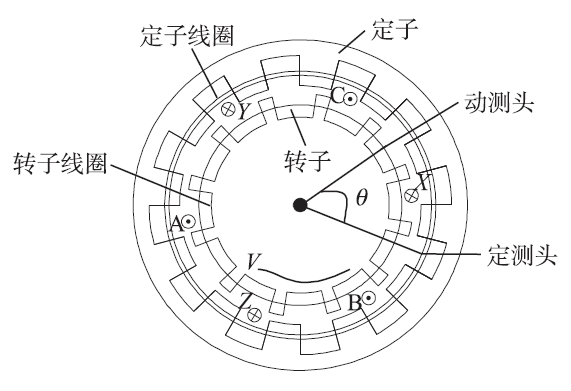
图1 圆型场式时栅结构

随着激励信号的改变，两相感应绕组按照如下表达式进行信号输出：

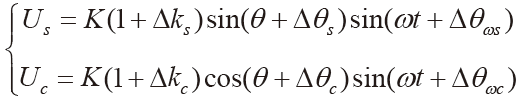(1)

式中， Δk_s与Δk_c表示两相感应信号对应的幅值差异；Δθ_s、Δθ_c表示两相感应信号产生的正交误差； Δθ_ωs与Δθ_ωc表示相位误差。通常可以将两路感应信号U_s、U_c之间的差值表示成以下合成信号：

U_e=U_s-U_c=KSin(θ−φ)sin(ωt) (2)

使感应产生的输出信号和初始信号间存在幅值差异。式（1）的Δk_s≠Δk_c，现假定只存在幅值差异，测量误差为e_k，得到ϕ=θ+e_k。再以一阶微量代替二阶微量，可以得到以下测量误差：

e_k=0.5(Δk_s−Δk_c)sin(2θ) (3)

根据以上分析结果可知，当时栅激励信号发生幅值与相位变化后，都会引起误差项e_k与e_ω，从而降低测试的准确性。

2 组合预测模型

可以利用BP 神经网络模型对长时间以及含有大量历史数据的时栅信号处理系统进行分析，采用灰色模型更加适合分析含有较少历史数据的时栅信号处理系统^[10-11]。为了更好地满足对该系统不同模块电路的运行状况进行测试的要求，可以发挥BP 神经网络模型所具备的时变捕捉以及非线性映射特性，同时利用G(1，1) 模型能够快速预测样本数量少和无规律数列的特征，综合发挥上述两种预测模型的优势，根据加权－比例－平均的处理方式，建立相应的加权平方以及平均组合模型，由此获得能够适应不同样本数量的预测模型，使预测模型达到更大适用范围并显著增大预测精度^[12]。

以Y₁（t）表示BP 神经网络的预测值，以Y₂（t）表示G（1，1）模型的预测值，结合实际预测条件计算加权系数ω1、ω2，两个系数应符合非负荷与归一化的条件。

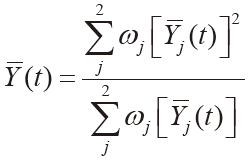t =1,2, ,n （4）

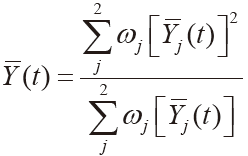t =1,2, ,n (4)

Y₁(t)与Y₂(t)都是属于BP 神经网络的预测参数，再利用二次规划方法得到ω₁与ω₂，从而预测出电路模块的实际值和预测值之间的最低偏差，由此得到以下所示的二次规划模型：

minJ't=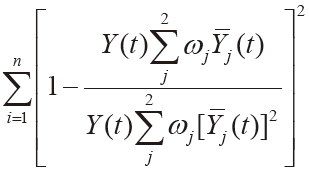 (5)

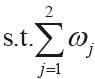t=1,2,3···n =1

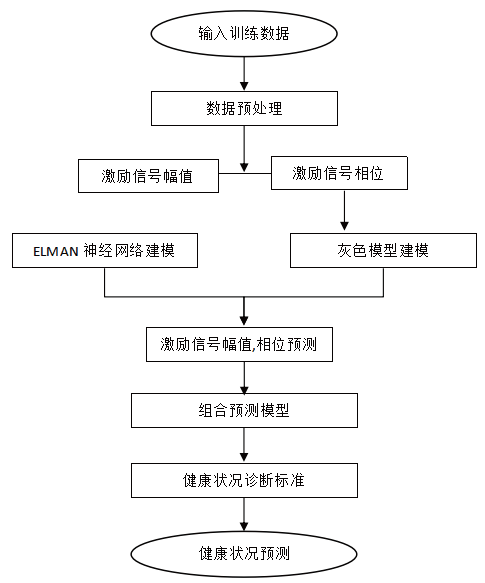
图2 健康状况预测流程图

3 预测模型建立

对圆型场结构的时栅传感器进行测试，用于测试的时栅信号处理系统实际健康状态是已知的，总共提供4个数据接口，构建了时栅传感器数据采集系统，按照6 h间隔条件从偏置电路、功率放大模块、滤波电路中采集输出数据，由于从现场进行数据采集需要花费很长的时间，因此从实验室的数据库内按照6 h 间隔对应的历史数据组成样本，分别从各电路模块中输出600 个数据进行测试，从中选择500 个数据组成训练模型，再以剩下的100 个对模型进行检验，利用该系统的10 d 内包含的数据对最后20 d 中的系统健康情况进行预测。

4 实验及讨论

在预测模型中输入预处理后的数据并完成训练以及测试过程。之后通过功率放大模块对激励信号幅值进行输出，根据实际测试结果判断系统预测精度。

通过计算得到表1 评价指标。模型相关系数R2 都高于98%，推断预测值和实际测试值基本相符，达到了较低的预测误差。

对上述两个模型获得的预测结果进行分析可知，第1个模型的预测效果比第两个模型更优。利用2 次规划模型计算得到组合模型ω1 与ω2 依次为0.7 与0.3。

较预测结果可知，组合模型产生的测试点比较靠近预测结果，达到了很高相关系数，误差也较低，由此可见，该模型可以满足预测要求，实现准确预测。

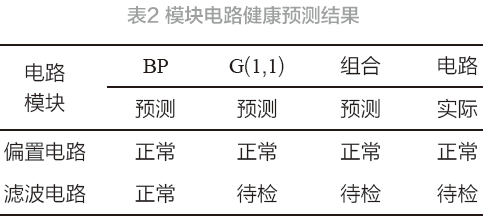
计算出两个参数的相对误差再跟健康诊断标准进行对比，得到模块电路健康预测结果见表2 所示。比较模型诊断数据与电路的实际健康情况，两种模型存在1 个模块发生诊断结果偏差的现象，采用组合模型能够实现所有模块健康状况的准确预测，获得比单一模型更优的预测精度。

5 结束语

本文设计了一种综合运用BP 神经网络与灰色模型进行预测的模型。根据激励信号的实际误差引起的测试精度变化，得到预测模型的各项参数。之后建立组合预测模型并设置了健康状况的参考标准。经测试发现，采用此健康预测模式可以实现高可靠性与高精度的预测效果，能够提前掌握电路系统的健康情况。

参考文献：

[1] 张永花,王玉芳.一次性信号放大电化学阻抗RNA传感器研究[J].化学研究,2019(2):140-146

[2] 周芳芳,毛索颖,黄跃文.基于双微处理器的传感器自动采集装置设计与实现[J].长江科学院院报,2019,36(6):157-160.

[3] 张天恒,王宇,梁敏,等.时栅传感器气隙磁导正弦规律变化的调制方法[J].传感技术学报,2022,35(10):1363-1367.

[4] 陈自然,卜敬,赵有祥,等.基于平面磁场的双列结构绝对式时栅传感器研究[J].传感技术学报,2021,34(4):463-469.

[5] 刘洋,武亮,彭东林,等.平面线圈型时栅传感器及动尺姿态误差特性分析[J].仪表技术与传感器,2020,454(11):21-27+32.

[6] 辛毅,徐洋,朱剑锋,等.基于PVDF压电薄膜的仿生触觉检测系统研究[J].压电与声光,2019,41(3):405-409.

[7] 王明辉,陈冰怀,黄海(王莹),等.自动气象站常规传感器现场检测系统设计[J].气象科技,2019,47(3):402-407.

[8] 汤自宁,吴瑾,王冠达,等.集成于车身控制器的胎压接收模块硬件设计[J].汽车电器,2019(6):37-39.

[9] 金燕,陈强.电子技术“口袋实验室”开发及实验项目设计[J].实验技术与管理,2019(6):94-99.

[10] 朱欢欢,李厚佳,张梦梦,等.基于BP神经网络的外圆磨削颤振在线识别和监测方法[J].金刚石与磨料磨具工程,2022,42(1):104-111.

[11] 杨风开.磁调制FFT传感器信号的神经网络处理方法[J].仪表技术与传感器,2019,440(9):96-100+126.

[12] 王丽影,郑艺华.量热式生物传感器信号降噪和穿透曲线的研究[J].仪表技术与传感器,2013,361(2):1-3+15.

（本文来源于《电子产品世界》杂志2023年6月期）